Download the notebook here!
Interactive online version:
Nonlinear Equations
Outline
Setup
Bisection method
Function iteration
Newton’s method
Quasi-Newton method
Choosing a solution method
Convergence
Resources
Setup
The nonlinear equation takes one of two forms.
Rootfinding problem Given a function
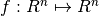 ,compute an
,compute an 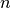 -vector
-vector 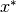 , called root of
, called root of  , such that
, such that 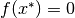 .
.Fixed-point problem Given a function
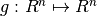 , compute an
, compute an 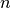 -vector
-vector 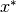 called fixed point of
called fixed point of 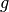 such that
such that 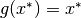
The two forms are equivalent.
A root of
 is a fixed-point of
is a fixed-point of 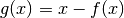 .
.A fixed-point of
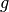 is a root ot
is a root ot 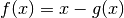 .
.
Nonlinear equations arise naturally in economics:
Multicommodity market equilibrium models
Multiperson static game models
Unconstrained optimization models
Nonlinear equations also arise indirectly when numerically solving economic models involving functional equations:
Dynamic optimization models
Rational expectations models
Arbitrage pricing models
Building on our earlier lab on the solution to linear systems of equations, often the solution to a nonlinear problem is computed iteratively by solving a sequence of linear problems.
sensitivity to intial condition
susceptible to rounding error
[2]:
# from temfpy.nonlinear_equations import exponential # noqa: F401
from scipy import optimize
import pandas as pd
import numpy as np
from nonlinear_algorithms import bisect
from nonlinear_plots import plot_bisection_test_function
from nonlinear_algorithms import fixpoint
from nonlinear_plots import plot_fixpoint_example
from nonlinear_plots import plot_newton_pathological_example
from nonlinear_plots import plot_convergence
from nonlinear_plots import plot_newtons_method
from nonlinear_plots import plot_secant_method
from nonlinear_algorithms import newton_method
from nonlinear_problems import bisection_test_function
from nonlinear_problems import function_iteration_test_function
from nonlinear_problems import newton_pathological_example
Bisection method
We start with the implementation (and testing) of the bisection algorithm.
The bisection method is perhaps the simplest and most robust method for computing the root of a continuous real-valued function defined on a bounded interval of the real line. The bisection method is based on the Intermediate Value Theorem, which asserts that if a continuous real-valued function defined on an interval assumes two distinct values, then it must assume all values in between. In particular, if
 is continuous, and
is continuous, and 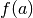 and
and 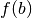 have different signs, then
have different signs, then
 must have at least one root
must have at least one root  in
in ![[a, b]](../../_images/math/e219413cc39d1f0e877b563af388435f55f73b68.png) .
.Each iteration begins with an interval known to contain or to bracket a root of
 , because the function has different signs at the interval endpoints. The interval is bisected into two subintervals of equal length. One of the two subintervals must have endpoints of different signs and thus must contain a root of
, because the function has different signs at the interval endpoints. The interval is bisected into two subintervals of equal length. One of the two subintervals must have endpoints of different signs and thus must contain a root of  . This subinterval is taken as the new interval with which to begin the subsequent iteration. In this manner, a sequence of intervals is generated, each half the
width of the preceding one, and each known to contain a root of
. This subinterval is taken as the new interval with which to begin the subsequent iteration. In this manner, a sequence of intervals is generated, each half the
width of the preceding one, and each known to contain a root of  . The process continues until the width of the bracketing interval containing a root shrinks below an acceptable convergence tolerance.
. The process continues until the width of the bracketing interval containing a root shrinks below an acceptable convergence tolerance.
[3]:
??bisect
Signature: bisect(f, a, b, tolerance=1.5e-08)
Source:
def bisect(f, a, b, tolerance=1.5e-8):
"""Apply bisect method to root finding problem.
Iterative procedure to find the root of a continuous real-values function :math:`f(x)` defined
on a bounded interval of the real line. Define interval :math:`[a, b]` that is known to contain
or bracket the root of :math:`f` (i.e. the signs of :math:`f(a)` and :math:`f(b)` must differ).
The given interval :math:`[a, b]` is then repeatedly bisected into subintervals of equal length.
Each iteration, one of the two subintervals has endpoints of different signs (thus containing
the root of :math:`f`) and is again bisected until the size of the subinterval containing the
root reaches a specified convergence tolerance.
Parameters
----------
f : callable
Continuous, real-valued, univariate function :math:`f(x)`.
a : int or float
Lower bound :math:`a` for :math:`x \\in [a,b]`.
b : int or float
Upper bound :math:`a` for :math:`x \\in [a,b]`. Select :math:`a` and :math:`b` so
that :math:`f(b)` has different sign than :math:`f(a)`.
tolerance : float
Convergence tolerance.
Returns
-------
x : float
Solution to the root finding problem within specified tolerance.
Examples
--------
>>> x = bisect(f=lambda x : x ** 3 - 2, a=1, b=2)[0]
>>> round(x, 4)
1.2599
"""
# Get sign for f(a).
s = np.sign(f(a))
# Get staring values for x and interval length.
x = (a + b) / 2
d = (b - a) / 2
# Continue operation as long as d is above the convergence tolerance threshold.
# Update x by adding or subtracting value of d depending on sign of f.
xvals = [x]
while d > tolerance:
d = d / 2
if s == np.sign(f(x)):
x += d
else:
x -= d
xvals.append(x)
return x, np.array(xvals)
File: ~/external-storage/sciebo/office/OpenSourceEconomics/teaching/scientific-computing/course/lectures/nonlinear_equations/nonlinear_algorithms.py
Type: function
Let’s visualize a test function to get a sense of what result can should expect.
[4]:
??bisection_test_function
Signature: bisection_test_function(x)
Source:
def bisection_test_function(x):
"""Get test function for bisection."""
return x ** 3 - 2
File: ~/external-storage/sciebo/office/OpenSourceEconomics/teaching/scientific-computing/course/lectures/nonlinear_equations/nonlinear_problems.py
Type: function
[5]:
??plot_bisection_test_function
Signature: plot_bisection_test_function(f)
Source:
def plot_bisection_test_function(f):
"""Plot bisect example."""
fig, ax = plt.subplots()
grid = np.linspace(1, 2)
values = []
for value in grid:
values.append(f(value))
ax.plot(grid, values)
ax.axes.axhline(0, color="grey")
ax.set_ylabel("f(x)")
ax.set_xlabel("x")
File: ~/external-storage/sciebo/office/OpenSourceEconomics/teaching/scientific-computing/course/lectures/nonlinear_equations/nonlinear_plots.py
Type: function
The ability to vectorize functions using np.vectorize comes in very handy when evaluating functions over a grid. However, be aware that this is a simple replacement of a
for loopand thus does not improve performance.
We are ready to go …
[6]:
plot_bisection_test_function(bisection_test_function)
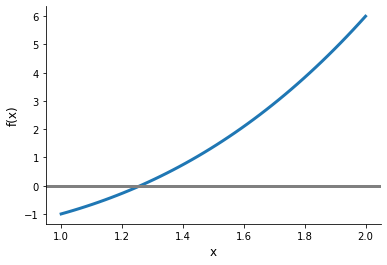
Now we are ready to check our implementation and investigate the sensitivity of results to alternative tuning parameter.
[26]:
lower, upper = 1, 2
x, xvals = bisect(bisection_test_function, lower, upper)
print(f"The root of our test function is {x:3.2f}.")
The root of our test function is 1.26.
Exercises
Write a short test that ensures that in fact found a root of the function.
Create a simple plot that shows each iterate of
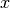 and label the two axis appropriately.
and label the two axis appropriately.
Function iteration
Function iteration is a relatively simple technique that may be used to compute a fixed point
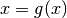 of a function from
of a function from 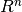 to
to 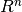 . The technique is also applicable to a rootfinding problem
. The technique is also applicable to a rootfinding problem 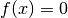 by recasting it as the equivalent fixed-point problem
by recasting it as the equivalent fixed-point problem 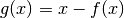 . Function iteration begins with the analyst supplying a guess
. Function iteration begins with the analyst supplying a guess 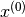 for the fixed point of
for the fixed point of 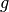 . Subsequent iterates are generated using the simple iteration rule
. Subsequent iterates are generated using the simple iteration rule
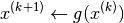
Since 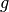 is continuous, if the iterates converge, they converge to a fixed point of
is continuous, if the iterates converge, they converge to a fixed point of 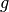 .
.
[8]:
??fixpoint
Signature: fixpoint(f, x0, tolerance=0.0001)
Source:
def fixpoint(f, x0, tolerance=10e-5):
"""Compute fixed point using function iteration.
Parameters
----------
f : callable
Function :math:`f(x)`.
x0 : float
Initial guess for fixed point (starting value for function iteration).
tolerance : float
Convergence tolerance (tolerance < 1).
Returns
-------
x : float
Solution of function iteration.
Examples
--------
>>> import numpy as np
>>> x = fixpoint(f=lambda x : x**0.5, x0=0.4, tolerance=1e-10)[0]
>>> np.allclose(x, 1)
True
"""
e = 1
xvals = [x0]
while e > tolerance:
# Fixed point equation.
x = f(x0)
# Error at the current step.
e = np.linalg.norm(x0 - x)
x0 = x
xvals.append(x0)
return x, np.array(xvals)
File: ~/external-storage/sciebo/office/OpenSourceEconomics/teaching/scientific-computing/course/lectures/nonlinear_equations/nonlinear_algorithms.py
Type: function
Let’s visualize a test function to get a sense of what result can should expect.
[9]:
??function_iteration_test_function
Signature: function_iteration_test_function(x)
Source:
def function_iteration_test_function(x):
"""Get test function for function iteration."""
return np.sqrt(x)
File: ~/external-storage/sciebo/office/OpenSourceEconomics/teaching/scientific-computing/course/lectures/nonlinear_equations/nonlinear_problems.py
Type: function
[10]:
plot_fixpoint_example(function_iteration_test_function)
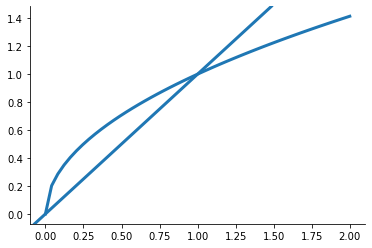
Let’s run and test our implementation.
[28]:
x = fixpoint(function_iteration_test_function, 0.4, tolerance=1e-5)[0]
try:
np.testing.assert_almost_equal(function_iteration_test_function(x), x)
except AssertionError as msg:
print(msg)
Arrays are not almost equal to 7 decimals
ACTUAL: 0.9999965046343594
DESIRED: 0.9999930092809364
This is an example of using a try-except block to explicitly handle the
AssertionError. Details on exception handling in Python, see this Wiki for some more examples.
We set two parameters manually, which one is it? How about choosing different starting values?
[33]:
for x0 in np.linspace(0.1, 0.9):
x = fixpoint(function_iteration_test_function, x0, tolerance=1e-5)[0]
try:
np.testing.assert_almost_equal(function_iteration_test_function(x), x)
print("Success for x0 {x0}")
except AssertionError:
pass
Let’s look at the tolerance setting instead.
Exercises
Find the fixpoint of
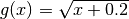 .
.How many iterations does the function iteration need? Does it depend on the starting value?
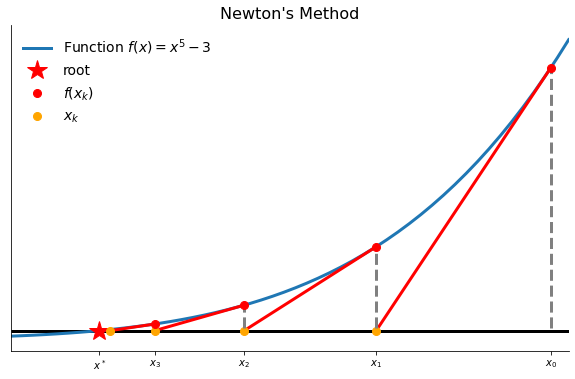
Newton’s method
Newton’s method is an algorithm for computing the root of a function 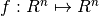 . Newton’s method employs a strategy of successive linearization. The strategy calls for the nonlinear function
. Newton’s method employs a strategy of successive linearization. The strategy calls for the nonlinear function  to be approximated by a sequence of linear functions whose roots are easily computed and, ideally, converge to the root of
to be approximated by a sequence of linear functions whose roots are easily computed and, ideally, converge to the root of  . In particular, the
. In particular, the 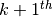 iterate
iterate
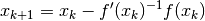
is the root of the Taylor linear approximation of  around the preceding iterate
around the preceding iterate 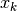 .
.
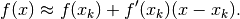
This yields the following iteration rule:
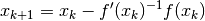
If 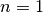 , the iteration rule takes the simpler form
, the iteration rule takes the simpler form
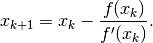
[13]:
plot_newtons_method()
Exercises
Plot the function
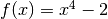 and provide a rough estimate of its fix point.
and provide a rough estimate of its fix point.Let’s compute the root of the function using Newton’s method by employing the proper iteration rule:
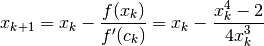
We now look at a more general implementation.
[14]:
??newton_method
Signature: newton_method(f, x0, tolerance=1.5e-08)
Source:
def newton_method(f, x0, tolerance=1.5e-8):
"""Apply Newton's method to solving nonlinear equation.
Solve equation using successive linearization, which replaces the nonlinear problem
by a sequence of linear problems whose solutions converge to the solution of the nonlinear
problem.
Parameters
----------
f : callable
(Univariate) function :math:`f(x)`.
x0 : float
Initial guess for the root of :math:`f`.
tolerance : float
Convergence tolerance.
Returns
-------
xn : float
Solution of function iteration.
"""
x0 = np.atleast_1d(x0)
# This is tailored to the univariate case.
assert x0.shape[0] == 1
xn = x0.copy()
while True:
fxn, gxn = f(xn)
if np.linalg.norm(fxn) < tolerance:
return xn
else:
xn = xn - fxn / gxn
File: ~/external-storage/sciebo/office/OpenSourceEconomics/teaching/scientific-computing/course/lectures/nonlinear_equations/nonlinear_algorithms.py
Type: function
Question
What are the important generalizations?
Let’ explore one last test function to test the interface of our function and learn something about private functions in the process.
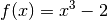
[36]:
def _jacobian(x):
return 3 * x ** 2
def _value(x):
return x ** 3 - 2
def f(x):
return _value(x), _jacobian(x)
x = newton_method(f, 0.4)
np.testing.assert_almost_equal(f(x)[0], 0)
A potential shortcoming of Newton’s method is that the derivatives required for the Jacobian may not be available may be difficult to calculate analytically, or time-consuming to approximate numerically … or that it might actually fail or result in cycles.
Consider the following pathological example which has a unique root at  .
.
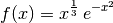
[37]:
??newton_pathological_example
Signature: newton_pathological_example(x)
Source:
def newton_pathological_example(x):
"""Get Newton Pathological example."""
fval = newton_pathological_example_fval(x)
fjac = newton_pathological_example_fjac(x, newton_pathological_example_fval)
return fval, fjac
File: ~/external-storage/sciebo/office/OpenSourceEconomics/teaching/scientific-computing/course/lectures/nonlinear_equations/nonlinear_problems.py
Type: function
[17]:
plot_newton_pathological_example(newton_pathological_example)
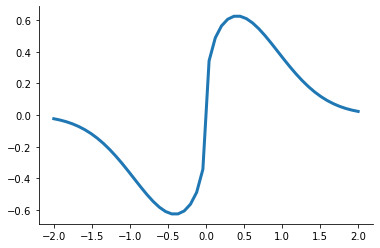
We can derive the Newton iterates as:
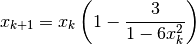
Questions
What happens when you apply Newton’s method to solve this function for different starting values?
What does the Newton iterate look like for very small and very large values?
For
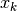 small, the iteration reduces to
small, the iteration reduces to 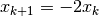 and so it converges to
and so it converges to  only if
only if 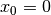 .
.For
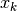 large, the iteration becomes
large, the iteration becomes
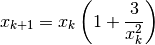
which diverges, but will eventually satisfy the stopping rule.
Another problems might be cycles.
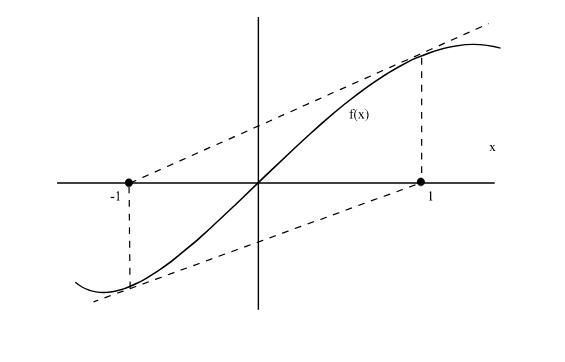
Quasi-Newton method
Quasi-Newton methods replace the Jacobian in Newton’s method with an estimate that is easier to compute. Specifically, quasi-Newton methods use an iteration rule
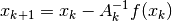
where 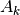 is an estimate of the Jacobian
is an estimate of the Jacobian 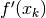 .
.
The secant method replaces the derivative in Newton’s method with the estimate
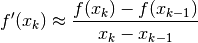
The secant method is so called because it approximates the function  using secant lines drawn through successive pairs of points on its graph.
using secant lines drawn through successive pairs of points on its graph.
[18]:
plot_secant_method()
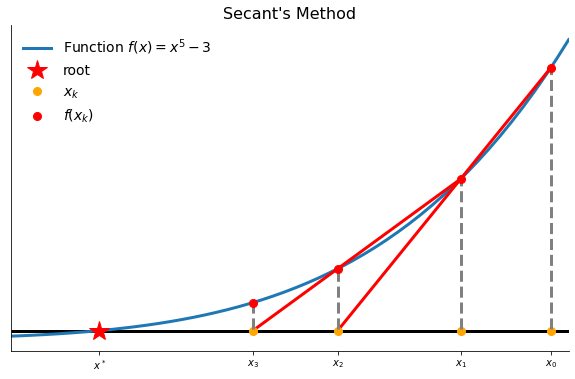
Let’s start with a crude implementation to make sure we understood the setup correctly. We will use this to show the lambda functions, see here for details.
[19]:
f = lambda z: z ** 4 - 2 # noqa: E731
x, xlag = 2.3, 2.4
for it in range(50):
d = (f(x) - f(xlag)) / (x - xlag)
x, xlag = x - f(x) / d, x
if abs(x - xlag) < 1.0e-10:
break
print(f"Root of our example function {x:5.3f}")
Root of our example function 1.189
Broyden’s method is the most popular multivariate generalization of the univariate secant method. Broyden’s method replaces the Jacobian in Newton’s method with an estimate 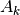 that is updated by making the smallest possible change (measured by the Frobenius norm) that is consistent with the secant condition:
that is updated by making the smallest possible change (measured by the Frobenius norm) that is consistent with the secant condition:
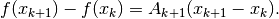
This yields the iteration rule
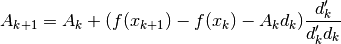
where 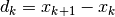 . Often
. Often 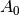 is equal to the numerical approximation of
is equal to the numerical approximation of  at
at 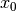 . The remarkable feature of Broyden’s method is that it is able to generate a reasonable approximation to the Jacobian matrix with no additional evaluations of the function. This approach is readily available in scipy.
. The remarkable feature of Broyden’s method is that it is able to generate a reasonable approximation to the Jacobian matrix with no additional evaluations of the function. This approach is readily available in scipy.
[20]:
rslt = optimize.root(f, 1.0, method="broyden1")
print(f"Root of our example function {rslt['x']:5.3f}")
Root of our example function 1.189
Consider a market with two firms producing the same good. Firm 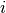 ’s total cost of production is a function of the quantity
’s total cost of production is a function of the quantity 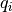 it produces.
it produces.
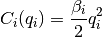
The market clearing price is a function of the total quantity produced by both firms.
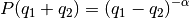
Firm 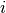 chooses production
chooses production 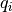 so as to maximize its profit taking the other firm’s output as given.
so as to maximize its profit taking the other firm’s output as given.
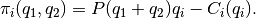
Thus in equilibrium,
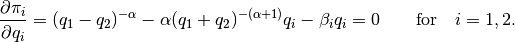
Exercise
Compute the market equilibrium quantities using Broyden’s method for
 and
and ![\beta= [0.6, 0.8]](../../_images/math/678a74729a1330286156f060b7d3708ac1fe01cb.png) .
.
Choosing a solution method
We now consider a more challenging task and compare the performance of scipy’s root finding algorithms. We will use one of temfpy’s test functions for this.
[21]:
??exponential
Object `exponential` not found.
Now let’s see which of the algorithms performs best for a ten dimensional problem.
[22]:
METHODS = ["broyden1", "broyden2", "anderson", "Krylov"]
DIMENSION = 10
PROBLEMS = 5
We are ready to run our benchmarking exercise.
[23]:
def exponential_function(x):
x = np.atleast_1d(x)
p = x.shape[0]
rslt = np.tile(np.nan, p)
for i in range(p):
xi = np.clip(x[i], None, 300)
if i == 0:
rslt[i] = np.exp(xi) - 1
else:
rslt[i] = (i / 10) * (np.exp(xi) + x[i - 1] - 1)
return rslt
np.testing.assert_almost_equal(exponential_function([0, 0]), [0.0] * 2)
columns = ["Algorithm", "Sample", "Success", "Iteration"]
df = pd.DataFrame(columns=columns)
for method in METHODS:
# Ensure that all have same test problems.
np.random.seed(123)
for _ in range(PROBLEMS):
x0 = np.random.uniform(size=DIMENSION)
rslt = optimize.root(exponential_function, x0, method=method)
info = [[method, _, rslt["success"], rslt["nit"]]]
df = df.append(pd.DataFrame(info, columns=columns), ignore_index=True)
/home/peisenha/.local/lib/python3.8/site-packages/scipy/optimize/nonlin.py:1016: RuntimeWarning: invalid value encountered in true_divide
d = v / vdot(df, v)
/home/peisenha/.local/lib/python3.8/site-packages/scipy/optimize/nonlin.py:1016: RuntimeWarning: divide by zero encountered in true_divide
d = v / vdot(df, v)
/home/peisenha/.local/lib/python3.8/site-packages/scipy/optimize/nonlin.py:771: RuntimeWarning: invalid value encountered in multiply
self.collapsed += c[:,None] * d[None,:].conj()
Now we can explore the performance of the alternative implementations.
[24]:
df.head()
[24]:
| Algorithm | Sample | Success | Iteration | |
|---|---|---|---|---|
| 0 | broyden1 | 0 | False | 1100 |
| 1 | broyden1 | 1 | False | 1100 |
| 2 | broyden1 | 2 | False | 1100 |
| 3 | broyden1 | 3 | False | 1100 |
| 4 | broyden1 | 4 | False | 1100 |
Convergence
Two factors determine the speed with which a properly coded and initiated algorithm will converge to a solution:
Asymptotic rate of convergence
Computational effort per iteration
The asymptotic rate of convergence measures improvement afforded per iteration near the solution. A sequence 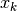 converges to
converges to 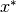 at an asymptotic rate of order
at an asymptotic rate of order 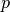 if there is constant
if there is constant 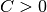 such that for
such that for 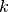 sufficiently large,
sufficiently large,
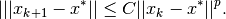
Function iteration converges at a “linear” rate with
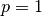 and
and 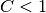 .
.Broyden’s method converges at a “superlinear” rate with
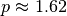 .
.Newton’s method converges at a “quadratic” rate with
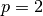 .
.
[25]:
plot_convergence()
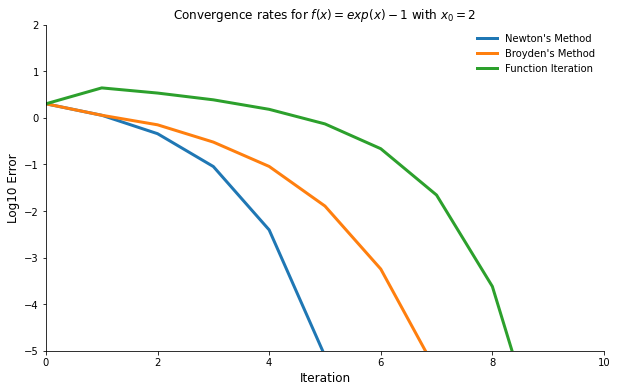
However, algorithms differ in computations per iteration.
Function iteration requires a function evaluation.
Broyden’s method additionally requires a linear solve.
Newton’s method additionally requires a Jacobian evaluation.
Thus, a faster rate of convergence typically can be achieved only by investing greater computational effort per iteration. The optimal tradeoff between rate of convergence and computational effort per iteration varies across applications.
Resources
HOMPACK: https://www.netlib.org/hompack