Functions
This module contains the algorithms for the linear equations lab.
The materials follow Miranda and Fackler (2004, [MF04]) (Chapter 2). The python code heavily draws on Romero-Aguilar (2020, [RA20]) and Foster (2019, [Fos19]).
- labs.linear_equations.linear_algorithms.backward_substitution(a, b)[source]
Perform backward substitution to solve a system of linear equations.
Solves a linear equation of type
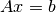 when for an upper triangular matrix
when for an upper triangular matrix
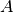 of dimension
of dimension 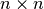 and vector
and vector 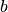 of length
of length 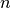 .
.- Parameters
a (numpy.ndarray) – Lower triangular matrix of dimension
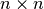 .
.b (numpy.ndarray) – Vector of length
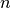 .
.
- Returns
x – Solution of the linear equations. Vector of length
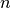 .
.- Return type
numpy.ndarray
- labs.linear_equations.linear_algorithms.forward_substitution(a, b)[source]
Perform forward substitution to solve a system of linear equations.
Solves a linear equation of type
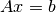 when for a lower triangular matrix
when for a lower triangular matrix
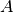 of dimension
of dimension 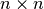 and vector
and vector 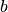 of length
of length 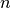 .
The forward subsititution algorithm can be represented as:
.
The forward subsititution algorithm can be represented as: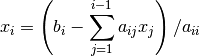
- Parameters
a (numpy.ndarray) – Lower triangular matrix of dimension
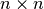 .
.b (numpy.ndarray) – Vector of length
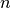 .
.
- Returns
x – Solution of the linear equations. Vector of length
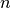 .
.- Return type
numpy.ndarray
- labs.linear_equations.linear_algorithms.gauss_seidel(a, b, x0=None, lambda_=1.0, max_iterations=1000, tolerance=1.4901161193847656e-08)[source]
Solves linear equation of type
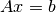 using Gauss-Seidel iterations.
using Gauss-Seidel iterations.In the linear equation,
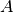 denotes a matrix of dimension
denotes a matrix of dimension
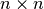 and
and 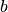 denotes a vector of length
denotes a vector of length 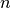 The solution
method performs especially well for larger linear equations if matrix :math`A`is
sparse. The method achieves fairly precise approximations to the solution but
generally does not produce exact solutions.
The solution
method performs especially well for larger linear equations if matrix :math`A`is
sparse. The method achieves fairly precise approximations to the solution but
generally does not produce exact solutions.Following the notation in Miranda and Fackler (2004, [MF04]), the linear equations problem can be written as
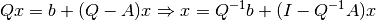
which suggest the iteration rule
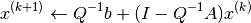
which, if convergent, must converge to a solution of the linear equation. For the Gauss-Seidel method,
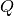 is the upper triangular matrix formed from the upper triangular elements of
is the upper triangular matrix formed from the upper triangular elements of
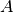 .
.- Parameters
a (numpy.ndarray) – Matrix of dimension
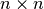
b (numpy.ndarray) – Vector of length
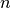 .
.x0 (numpy.ndarray, default None) – Array of starting values. Set to be if None.
lambda (float) – Over-relaxation parameter which may accelerate convergence of the algorithm for
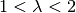 .
.max_iterations (int) – Maximum number of iterations.
tolerance (float) – Convergence tolerance.
- Returns
x – Solution of the linear equations. Vector of length
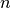 .
.- Return type
numpy.ndarray
- Raises
StopIteration – If maximum number of iterations specified by max_iterations is reached.
- labs.linear_equations.linear_algorithms.naive_lu(a)[source]
Apply a naive LU factorization.
LU factorization decomposes a matrix
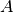 into a lower triangular matrix
into a lower triangular matrix 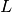 and upper triangular matrix U. The naive LU factorization does not apply permutations to
the resulting matrices and thus only works reliably for diagonal matrices
and upper triangular matrix U. The naive LU factorization does not apply permutations to
the resulting matrices and thus only works reliably for diagonal matrices 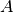 :
:- Parameters
a (numpy.ndarray) – Diagonal square matrix.
- Returns
l (numpy.ndarray)
u (numpy.ndarray)
- labs.linear_equations.linear_algorithms.solve(a, b)[source]
Solve linear equations using L-U factorization.
Solves a linear equation of type
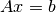 when for a nonsingular square matrix
when for a nonsingular square matrix
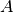 of dimension
of dimension 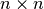 and vector
and vector 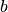 of length
of length 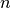 . Decomposes
Algorithm decomposes matrix
. Decomposes
Algorithm decomposes matrix 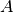 into the product of lower and upper triangular matrices.
The linear equations can then be solved using a combination of forward and backward
substitution.
into the product of lower and upper triangular matrices.
The linear equations can then be solved using a combination of forward and backward
substitution.Two stages of the L-U algorithm:
1. Factorization using Gaussian elimination:
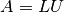 where
where 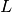 denotes
a row-permuted lower triangular matrix.
denotes
a row-permuted lower triangular matrix. 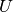 denotes a row-permuted upper
triangular matrix.
denotes a row-permuted upper
triangular matrix.2. Solution using forward and backward substitution. The factored linear equation of step 1 can be expressed as
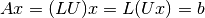
The forward substitution algorithm solves
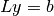 for y. The backward substitution
algorithm then solves
for y. The backward substitution
algorithm then solves 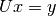 for
for 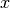 .
.- Parameters
a (numpy.ndarray) – Matrix of dimension
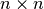
b (numpy.ndarray) – Vector of length
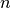 .
.
- Returns
x – Solution of the linear equations. Vector of length
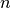 .
.- Return type
numpy.ndarray
Example
>>> b = np.array([1, 2, 3]) >>> a = np.array([[4, 0, 0], [0, 2, 0], [0, 0, 2]]) >>> solve(a, b) array([0.25, 1. , 1.5 ])